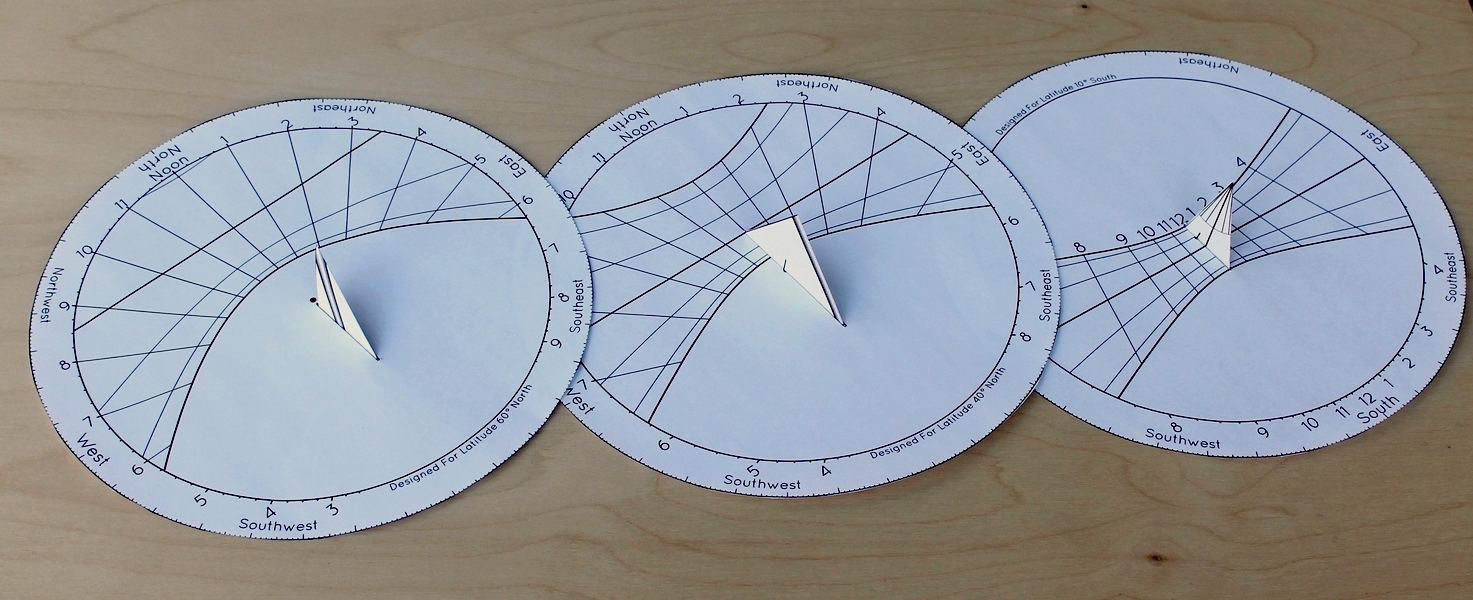
Butterfly Sundials
If you trace the path of the shadow of a vertical post throughout the day, what shape is the path? A "gnomonic" or "butterfly" sundial can track the sun through the seasons as well as the hours, by following the shadow of a vertical stick.
Ancient Greek stone-carvers created what were probably the first scientific instruments in history. Their sun-tracking devices followed the motion of the sun across the sky, reflecting the geometry of the sky downward and capturing it in beautiful stone sculptures. With gradation marks, these models in stone of the sky above could track not only the changing hours of the day, but also the progression of the seasons from one solstice to the next.
This simple paper sundial is my own updated version of a classic Ancient Greek sun-tracking instrument.
How the “Butterfly Sundial” Works
What happens if you just place a vertical stick or pole in the ground, and watch the shadow through the course of a day? Will the shadow trace out a circle around the pole, like the hand of a clock? Will the shadow pass in a straight line from the west to the east, as the sun passes overhead from the east to the west? Come to think of it, does the sun ever actually go straight overhead at any time of the day?
These are questions that a student or teacher could investigate and answer first-hand by following shadows across the ground. That would make a good educational activity. But if you are ok with me giving away plot spoilers, then read on.
For those of us who live in the northern hemisphere, the sun appears to move in an arc across the sky, but the arc is not straight up-and-down. It is tilted into the southern sky. So the shadow of a post follows neither a circle around the post, nor a straight line through the post, but something in between. It traces out a curve around the north side of the post. And the sun never at any time goes straight overhead (unless you live near the Equator). If it did, there would be a time during the day when the post had no shadow, and we never see a vertical post in sunshine without a shadow. There is a special time of day when the shadow is shortest, but the shadow never goes away completely.
What about summer or winter, when the sun is higher or lower? During the summer, the sun goes higher in the sky, so the shadows will be shorter and will follow a curve that passes closer to the pole. During the winter, the sun stays lower in the sky, so the shadows will stay longer and the curve will lie farther from the pole.
Altogether, if we follow the tip of the pole's shadow across the ground, trace out the curve that is formed in different seasons of the year, and record them permanently on the ground somehow, we will see a pattern like this:
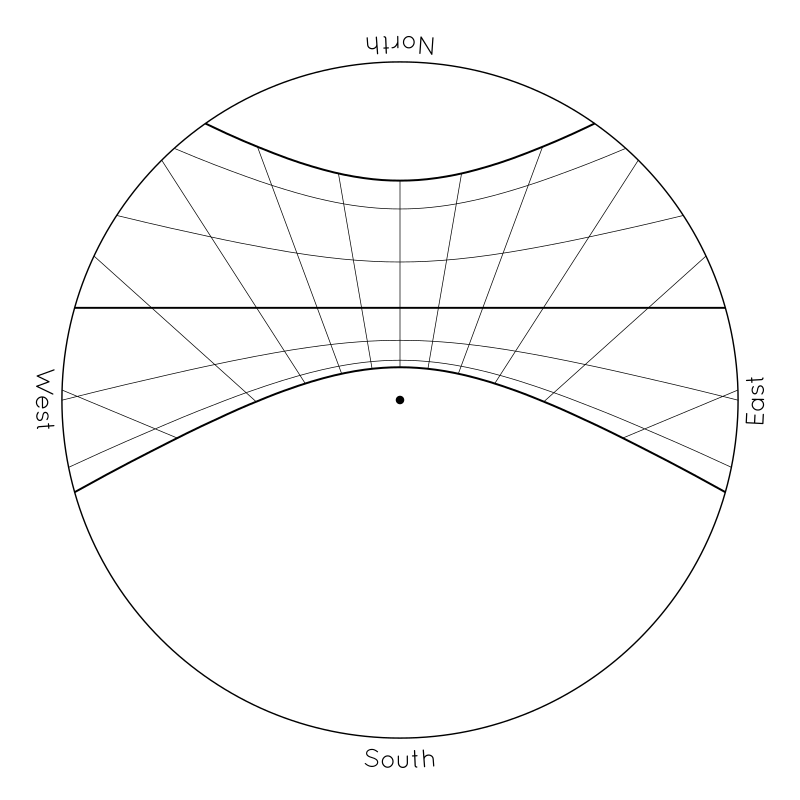
The sideways curves represent the path of the pole's shadow across the ground in different seasons of the year. Each day, the tip of the pole's shadow will follow one of these curves. It will start the day on the left/west side of the diagram as the sun rises in the east, it will shorten and pass to the north of the pole at noon, and then it will stretch out towards the east in the afternoon as the sun descends in the west. The innermost curves, the ones closest to the pole, represent the path of the shadow in summer, when the sun passes high across the sky. The outermost curves, the ones farthest from the pole, represent the path of the shadow in winter, when the sun stays lower in the sky and shadows are always elongated.
(Curiously, the curves will have different shapes depending on where you live and what season it is, but the path of the shadow in the spring and fall will always be a straight line, for some reason. And, as the ancient Greek masters of geometry realized, all of the curves, no matter the location or the season, are always conic sections. The spring/fall curve is always a straight line, because it is formed by the intersection of two planes. The others are hyperbolas and are formed by the intersection of a plane and a cone. The formation of conic sections on sundials would make a fascinating lesson by itself, but it requires you to visualize spheres and cones and planes overlapping in space, and I'll leave that as a different lesson for a different day...)
To be exact, the bounding curves at the northerly and southerly extremes represent the shadow paths on the solstices — those two days of the year when the sun reaches its northernly or southerly limit for the year, turns around, and starts heading back in the opposite direction towards the opposite pole. (The word “sol-stice” comes from from Latin roots meaning “the sun's standstill” or “the station of the sun”.) The straight line across the middle represents the path of the shadow on the equinoxes — those two special days in the spring and fall when the sun rises due east, sets due west, and divides the day and night into two equal halves of 12 hours each. (The word “equi-nox” derives from Latin roots meaning “equal night.”) The thinner intermediate curves represent one-month intervals between the solstices and equinoxes. Like a pendulum or a child on a swing set, the sun moves quickly through the equinoxes in the middle, and turns around slowly at the two outer limits, so the monthly curves are more closely spaced in summer and winter than they are in spring and fall. Depending on how closely you watch, the shadow will stay near the solstice curves for several weeks in the middle of summer and winter, while you might notice differences every few days in spring and fall.
The radial lines do not represent the direction of the shadow of the vertical stick. If you extend them all so that they intersect, they will not meet at the base of the vertical pole, but at a special place called the “sundial center”. If you imagine a line in space from this sundial center across the tip of the vertical pole and then extend it into outer space, it will point towards the North Star (or more precisely the North Celestial Pole). That tilted line in space represents the axle or axis around which everything spins. (And the angle of tilt will equal your latitude.) Instead, the radial lines on the disk represent equal intervals of time. The tip of the shadow will pass each of these marks at the rate of one per hour, and it will always lie on the same line at the same time of day, regardless of season. These radial lines represent the hours of the day, just like they do on a normal “garden variety” sundial. (Like the equinox line, they are straight because they are formed by the intersection of two planes.) The vertical mark in the middle represents noon. More precisely, it represents solar noon, the geometric “center” of the day, when the sun is at the highest point of its arc, shadows of vertical objects point due north, and the daylight is exactly half gone. The angled marks to the left and right of the noon mark represent one-hour intervals on either side of noon. (A sundial like this can't capture all of the hours of the day, because it would have to reach all the way to the horizon to do that. But you can still get a sense for how much shorter the days are in the winter than the summer by counting how many hours lie along each of the two solstice curves. And you can get a sense for how much lower the sun is in winter by how much farther the curve lies from the central pole.)
The entire grid or “butterfly” pattern represents a sort of mirror image, a reflection on the ground of the sun's “highway” across the sky, through the various hours of the day and the seasons of the year. These marks on the ground are like a “sky graph” that permanently captures the track of the sun across the sky, and the shadow of the pole is like the needle of a dial that shows you where the sun is in the sky right now.
The Ancient Greeks made sundials like this. They carved beautiful “sun recorders” in stone, and they mounted them in the agora so that everyone in the polis could measure the sun and track the seasons and the hours of the day. When they decided that they needed a special name for these special things, they were struck by the resemblance of the marks on the ground to the head of a double-bladed axe. So they chose the word “pelekinon”, which was their word for a double-sided axe, as their name for this kind of device. While I was developing these paper versions, I called them “Pelekinon Sundials” for lack of a better name, and I still often use that word in my own mind when thinking about them. But it's a very obscure word, and now I think I like the name “Butterfly Sundial” better. So that's the name I am choosing to use. What do you think?
By the way, I originally chose the name “Butterfly Sundial” for my paper creations, because I thought it would be colorful and unique. But I have since discovered, to my delight, that there is a large cadran solaire papillon in central Paris! In the picture, the upper diagonal of the triangle is parallel to the Earth's axis, the bottom corner rests at the “dial center” from which all radial lines emanate, and if you were to extend it upwards into outer space, you would find that it points at the North Star.

Also, it doesn't go by the name “Butterfly Sundial”, but you can see a similar example of a gnomonic sundial in Colorado Springs, next to the Chinook Trail Elementary School. (The official mathematical name for such sundials is “gnomonic sundial”. You can find more examples by performing an internet search, but the literature explaining them is fairly sparse.)

The Map
It would not surprise me if the Ancient Greeks thought about putting maps on their sundials, but they never actually did so. For one thing, it would have been quite difficult for them to carve irregular coastlines in stone. But more importantly, they didn't even have a complete map of the world. They knew it was a sphere, but they only knew a small portion of the surface. Whatever lay outside of the Mediterranean region was a complete mystery. Imagine knowing that you live on a sphere, but not knowing what's on the other side!
In the modern world, however, we have detailed maps of the entire surface of the sphere, and drawing them with a computer is relatively easy. So I tried putting maps on my sundials.
Why would you put a map on a sundial? Because something remarkable happens if you line up the map of the world around you in a special way on your sundial. Notice what happens if you center yourself in the map, turn it backwards so that north faces south, and stretch out the edges of the map in the same way that shadows are stretched out when the sun is low:
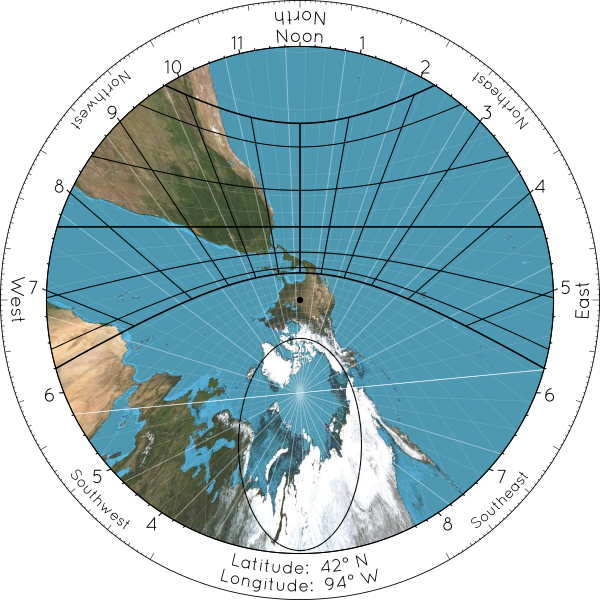
If you draw a map in the right way on a Butterfly Sundial, then the summer solstice curve of the sundial becomes the Tropic of Cancer on the map, the winter solstice curve lines up with the Tropic of Capricorn, and the equinox line becomes the Equator. (Again, I'm assuming that you live in the Northern Hemisphere. If you live in the Southern Hemisphere, reverse the words “summer” and “winter”. If you live near the equator, where the seasons are much less significant, replace “summer” with “June” and “winter” with “December”.) The “Pelekinon” or “Butterfly” on the sundial, i.e. the region where the shadow can land, lines up with the “Tropics” or “Tropic Belt” on the map, i.e. the part of the world where the sun can be directly overhead.
| Sundial | Map | |
| June Solstice Curve | → | Tropic of Cancer |
| Equinox Curve | → | Equator |
| December Solstice Curve | → | Tropic of Capricorn |
And best of all, at any given moment, wherever the shadow lands on the map shows the location in the world where the sun is directly overhead at that moment. With a properly arranged map, your sundial can not only track the sun's progress across your sky, it can also show you the sun's progress around the world.
(If you are interested in technical geometrical things, this way of drawing maps is called gnomonic projection after the “gnomon” of a sundial, and the place in the world where the sun is directly overhead is technically known as the subsolar point. Incidentally, the equator, all meridians, and any other “great circle” on the globe, always become straight lines in a gnomonic projection. This means that if you draw a straight line between any two points on the map, you will be drawing the shortest journey around the globe between those two points. Sometimes pilots and navigators use gnomonic projection maps to help them plot courses. They look weird, but they can be quite useful.)
I have added a few other decorations to the map that I thought would be interesting. The black ellipse (another conic section) is the Arctic Circle. The white lines mark out a grid, with a spacing of 5° between all grid lines. If you count the number of “parallels” from the equator to the dot in the center of the picture above, you should find a little more than 8 grid lines, or 40° of latitude, because Des Moines lies at a latitude of about 42° North. If you count the number of radial lines from Des Moines clockwise or counter-clockwise to any other location, you will be measuring the difference in longitude. Every third longitude line is emphasized, and one in particular is extra-white. As you might guess, the whitest white line is the Prime Meridian (and its antipode), dividing the world into Eastern and Western Hemispheres. The other emphasized lines divide the world into 24 slices, each 15° thick, or 1/24th of a full turn. These are the centerlines of the world's time zones. You can count how many hours separate you from other locations in the world by counting these lines. If you are interested in comparing your sundial's “solar time” to civil clock time, you should also pay attention to the discrepancy between the black noon line of your sundial, and the time zone centerlines on the map. The farther your time zone's centerline is from your sundial's noon line, the farther apart your clocks will be from your sundial. (As you can see in the example above, Des Moines lies about 4° to the west of the centerline of Central Time Zone, so clocks in Des Moines will all be about 15 minutes ahead of the sun, on average.) And the place where all the meridians meet is, naturally, the North Pole. The “sundial center” of the sundial becomes the North Pole on the map (or the South Pole, if you live in the Southern Hemisphere).
For example, the following picture shows a sundial made for central Iowa, in the sunshine at about 1:30 in the afternoon, about a month after the winter solstice. At the moment the picture was taken, the sun was somewhere over the South Pacific Ocean.
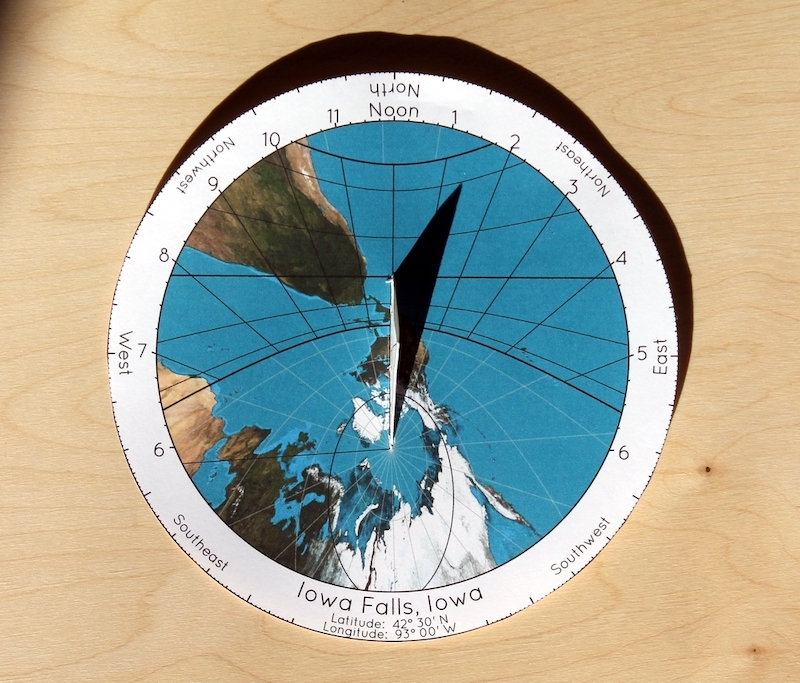
In an earlier article, I lamented the fact that we don't have more of these sorts of things in our parks and playgrounds. Part of the reason we don't is that they can't be mass-produced. Each one must be custom designed for the location in which it is to be used. This is obviously true for the map, because your location must be centered in the map. But even for plain Butterfly Sundials without a map, the positioning of the curves must match your latitude. All sundials must be designed for the latitude in which they are to be used, because the tilt of the sun's circle in your sky depends on your latitude. And if you want to put a map on your sundial, then the design will depend on your longitude as well. So a sundial with a map on it would have to be custom-designed for your exact location.
Unfortunately, the map for every sundial needs to be custom-designed for that sundial's location. I'm hoping to make a web app available someday that will allow everyone to generate a design for their own city. In the meantime, I'm offering black-and-white versions, without maps, to the general public. Read on to find instructions and download links.
Making the Sundial
My paper hemispherical sundial is very elaborate and time consuming to make. In contrast, this Butterfly Sundial is pretty easy. There isn't much to it — just two parts, three folds, and a little tape or glue. Start by choosing the design for the latitude closest to your own.
Next, print the design onto paper, preferably a medium-weight card stock. After you print out the design, cut out the circle of the dial around the perimeter, and then use a hobby knife to remove the slot in the middle. Before cutting out the gnomon, it will be helpful to score the fold lines with a ruler and a pin or something. Then cut out the gnomon, fold it, insert it through the slot in the disk, and tape or glue it into place. Depending on your latitude, your gnomon should look like one of these after it has been cut out and folded:

It is possible to insert the gnomon backwards. How do you know which way is the right way? The important thing to remember is that the tip of the gnomon needs to be centered over the circle of the sundial. In these paper sundials, the tip of the triangle replaces the top of a pole as the thing casting the shadow. The decorations are not meant to represent the vertical pole, but either the axis or the equator, depending on latitude. For most latitudes, there will be a small black mark on the base of the gnomon which should line up with the black dot in the center of the dial. This black mark is where the base of the hypothetical vertical pole would be. When assembled, your sundial should resemble one of these: